DZY has a $n \times n$ square matrix which is used to Orz JRY. Every morning,
DZY always finds $n^2$ people with distinct height, and they form a square matrix. Let person $i$ denote the $i$-th shortest person.
When they start to Orz JRY, JRY smiles and starts waving to them. JRY has a requirement. If he looks straight at the $i$-th column, he can see exactly $a_i$ people. If the person $i$ stands in front of the person $j$ and $i>j$, person $j$ is blocked.
JRY wants to know how many different matrices they can form, so he asked DZY to tell him the answer.
Now, DZY is asking you to work out the result.
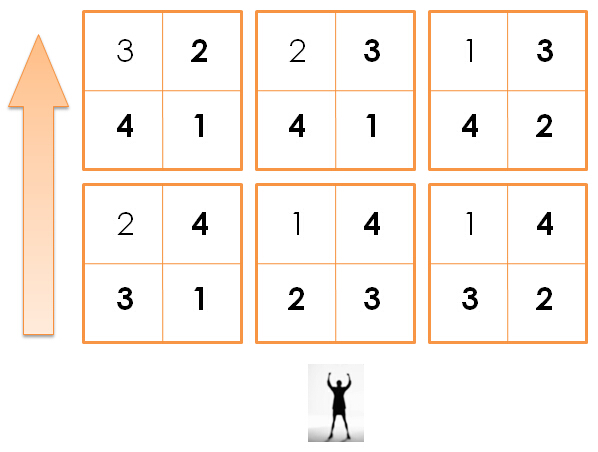
Input
The input consists several test cases.($TestCase\leq 5$)
The first line contains a integer $n(1\leq n\leq 10^5)$.
The second line, $n$ integers $a_i(1\leq a_i\leq n)$.
Output
For each query, please print a line containing a number representing the answer modulo $(10^9-51711)$.
Sample Input
2
1 2
3
2 1 1
7
2 4 3 5 2 4 3
Sample Output
6
20160
67779489
Hint
query 1. There are 6 possible ways in the picture.