第一次出题，对于时限的设置太过严格了（只开了标程的两倍），给大家说声对不起QwQ ##1001 By NanoApe 构成四边形的条件：最长边小于其余三条边的和 坑点1：假如有条长度为0的边的话，哪里来的四条边呢？ 坑点2：其余三条边的和会爆longlong，我们可以将a+b+c>d换成a>d-b-c来求解 ##1002 By YJQ 我们令dp[i][j]表示在前i个数中，选出若干个数使得它们的gcd为j的方案数，于是只需要枚举第i+1个数是否被选中来转移就可以了 令第i+1个数为v，当考虑dp[i][j]的时候，我们令$dp[i+1][j] += dp[i][j]$(v 不选),$dp[i+1][gcd(j,v)] += dp[i][j]$(v 选) 复杂度O(N*MaxV) MaxV 为出现过的数的最大值 其实有O(MaxV *log(MaxV))的做法，我们考虑记f[i]表示从这些数中选择若干个数，使得他们的gcd是i的倍数的方案数。假如有K个数是i的倍数，则f[i]=2^K-1，再用g[i]表示从这些数中选择若干个数，使得他们的gcd是i的方案数，则g[i]=f[i] - g[j] (对于所有j是i的倍数)。 由调和级数可以得到复杂度为O(MaxV *log(MaxV)) ##1003 By NanoApe 首先N的范围那么大是唬人的，真实的N的最大值大概也就A而已（大于A怎么可能还有数满足数字不重复啊） 算法一：直接搜索出满足数字不重复的所有数，然后再来看看满足k倍数的有多少个 然而这样做是O(A!)的，TLE 算法二：设F[S][o]表示当前用掉的数字的集合为S（二进制表示）且%k=o的方案数有多少 复杂度O(2^A*k)，爆炸 算法三：直接暴力算出k倍数的数，判断数字是否不重复 复杂度O(A^n/k)，爆炸 算法四：算法二+算法三，k小的时候用算法二，k大的时候用算法三 阀值试了试在23333左右挺不错的 算法五：预处理出所有进制中长度为[1,(长度+1)/2]的数，然后每次询问用meet in the middle处理 以找长度11的的数串为例，每次枚举模板C(11,5)*找与模板相对的，合适的数P(6,6)+枚举符合模板的合适的数P(11,5)*二分找解log(P(6,6)) 后记： 由于出题人实在是太过傻，导致算法二的复杂度分析错误，正确应该是O(2^A*A*k)，但是加优化完实测跑得飞快也是………… ##1004 By NanoApe 由于字符串长度最多为1000，不同的询问最多也只有500500种，那么我们先把所有询问的答案预处理出来即可。 从小到大枚举左端点，再从小到大移动右端点，用回文树维护本质不同的回文子串。 设我们现在枚举的区间是[l,r]，下一步是[l,r+1]，那么就相当于在回文树所维护的字符串的后面添加一个字符。当左端点改变时，重建回文树。 复杂度O(n^2) 其实还可以用manacher，在扩展的时候用Hash去重，复杂度O(n^2) ##1005 By YJQ 首先可以将问题转化为求有多少个不同的S的子串Sf，使得Sf的所有不同的位置都经过i，我们记为g[i]，那么每个i的答案为原串的不同子串个数-g[i] 我们考虑使用后缀自动机来解决此题，对于每个节点v，记录v的right集合的最小值Min和最大值Max，可以发现，假如一个子串Sb的出现最小位置为Min，最大位置为Max，Sb的长度为len，我们可以分类讨论这个串对g数组的贡献 1：Max-len>=Min，此时不会对g数组有贡献，因为这两个位置的串并不会相交 2：Max-len<Min，此时对所有Max-len<=i<Min的g[i]有1的贡献 但是S的本质不同的子串个数是N^2级别的，无法承受。但我们知道，共用一个right集合的串的len为一个连续的区间，这样我们对于每个节点进行讨论，可以发现每个节点对g数组的贡献会是先加一个等差数列，然后区间加一个相等的数，讨论过程略，注意边界情况。 这样我们可以使用树状数组或线段树等结构进行处理，复杂度O(NlgN),但还不够优化 由于所有的询问可以离线，我们可以利用差分序列，那么区间加同一个数可以变成在差分序列上的单点修改，区间加等差数列类似，可以再开一个差分序列记录覆盖i的有几个等差数列，公差的和是多少。最后求一遍前缀和就好了，复杂度O(N) 另外，Claris老司机提出了使用后缀树的做法，但是后缀树貌似常数比较迷的，可能会被卡

##Problem 1001 我们考虑集合中的每个数x对答案的贡献。 设集合有n个数，则包含x的子集个数有2^(n-1)个。 那么当n > 1时，x出现了偶数次，所以其对答案的贡献就是0；当 n = 1时，其对答案的贡献是 x。 ##Problem 1002 首先，如果不止一个字符出现的次数为奇数，则结果为0。 否则，我们把每个字符出现次数除2，也就是考虑一半的情况。 那么结果就是这个可重复集合的排列数了。 设该集合有n个数，第i个数出现次数为ai，那么结果就是 $fact(n)/fact(a_1)/fact(a_2)/..../fact(a_n)$。 ##Problem 1003 这是一个连通性的问题。你会发现如果将所有操作逆序来看的话就很容易用并查集来处理了。 首先把所有的山峰都加到图中，然后逆序处理每个操作： 对某次操作，在图中删除该位置的山峰，然后判断两个点是否联通，一旦联通就得到了结果。 这里需要对China和India分别新建一个对应的节点。 ##Problem 1004 先不考虑将结果乘以 1e6。 设 dp[i] 为从前 i 个格子的状态可以获得的最大破坏指数。那么我们可以枚举每个炸弹，该炸弹向左延伸的距离和向又延伸的距离。 设第 i 个炸弹破坏区间为 [l, r], 则 dp[r] = dp[l - 1] * log2(r - l + 1)。答案就是 dp[n - 1]。不要忘记最后要向下取整。 ##Problem 1005 首先将数列中所有满足条件的三元组处理出来，数量不会超过 $n$ 个。 设 pre[i] 为第 i 个三元组前一次出现的位置，如果在前面没有出现过则设为0,对于不合法的三元组，pre[i]设为 n。 这样对于一个查询 [L, R], 我们只不需要计算出 在这个区间内有多少个三元组的 pre 值是小于 L 的。 到这里，就可以使用可持久化线段树来计算了。

## 1001 因为数据规模很小，所以直接用$O(n^2)$时间求出有多少对$(i,j)$满足$a_i<a_j$，然后再除以$n(n-1)/2$即可。 当然也有$O(n\log n)$的做法，也很简单。 时间复杂度$O(n^2)$。 ## 1002 记$sum(a,k) = a + (a+1) + \cdots + (a+k-1)$。 首先，有解的充要条件是$sum(1,k) \le n$（如果没取到等号的话把最后一个$k$扩大就能得到合法解）。 然后观察最优解的性质，它一定是一段连续数字，或者两段连续数字中间只间隔1个数。这是因为$1\le a<=b-2$时有$ab<(a+1)(b-1)$，如果没有满足上述条件的话，我们总可以把最左边那段的最右一个数字作为$a$，最右边那段的最左一个数字作为$b$，调整使得乘积更大。 可以发现这个条件能够唯一确定$n$的划分，只要用除法算出唯一的$a$使得$sum(a,k)\le n < sum(a+1,k)$就可以得到首项了。 时间复杂度$O(\sqrt {n} )$，这是暴力把每项乘起来的复杂度。 ## 1003 对于每个结点$i$，统计出$f[i]$表示包含$i$的连通集有多少个，那么容易看出答案就是所有$f[i]$的和。 要计算$f[i]$是经典的树形DP问题。令$g[i]$表示以$i$为根的连通集的数目，那么$g[i]=\prod_j (g[j]+1)$，$j$是$i$的儿子，按这个从下往上DP一遍。 然后再用同样的式子从上往下DP一遍就好了。这一步骤写的时候要注意一下不要写错。 时间复杂度$O(n)$。 ## 1004 记$l=\log_2 \max\{n,m\}$。 枚举$i \text{ AND } j$和$i\text{ OR }j$的值分别是多少，因为是有包含关系的，所以枚举量是$3^l$的，用枚举子集的方法。 然后要计算有多少组$i,j$满足$i \text{ AND } j=a$, $i\text{ OR }j=b$, 且$1\le i \le n, 1\le j\le m$。$i$和$j$肯定都包含了$a$，剩下$b-a$的那些bit要分配给$i$和$j$，你可以算出最大分配多少才能使$i$不超过$n$，$j$也是同理，于是就确定了一个区间，区间内的都是合法的方案。 所以总的复杂度就是$O(l \times 3^l) = O(n^{1.59} \log n)$ claris老司机提供了一个$O(3^l)$的做法。考虑数位dp，状态是$f[i][and][or][2][2]$，这样的状态数是$1+3+\cdots + 3^l=O(3^l)$的，然后转移也可以$O(1)$。求gcd也不需要log，可以用一个$O(n)$预处理支持$O(1)$询问的结构，见http://mimuw.edu.pl/~kociumaka/files/stacs2013_slides.pdf 。 这题用奇妙的打表或者其他更加厉害的做法也是有可能AC的。 ## 1005 这是一道良心的基础数据结构题。 我们二分$a[k]$的值，假设当前是$mid$，然后把大于$mid$的数字标为$1$，不大于$mid$的数字标为$0$。然后对所有操作做完以后检查一下$a[k]$位置上是$0$还是$1$。 因为只有两种值，所以操作还是不难做的。只要用一个线段树，支持区间求和、区间赋值即可。这样要排序一个区间时只要查询一下里面有几个$1$和几个$0$，然后把前半段赋值为$0$，后半段赋值为$1$即可（降序的话就是反过来）。 复杂度是$O(m\log ^2 n)$的。 这题用其他玄学做法或者用更加厉害的平衡树做法也是有可能AC的。

1001, 1002, 1004 来自 Sengxian. 其余全部来自 Fuxey. ## 1001 - King's Cake 显然这很像求最大公约数的过程嘛，看这张神图：  所以每次 $\gcd$ 的时候累加答案即可，复杂度 $O(\log\max(n, m)T)$。 当然你要是循环减应该也放过了。 ## 1002 - King‘s Phone 一个简单的模拟题，首先判断序列长度是否合法，接着判断 $s_i$ 是否在 $[1, 9]$，最后扫一遍看看有没有重复以及跨过中间点的情况即可。 复杂度：$O(nT)$。 ## 1003 - King's Order 数一个长度为 $n$ 的序列 ， 并且序列中不能出现长度大于 $3$ 的连续的相同的字符 ， 这玩意就是一个数位DP嘛。 定义 $d[i][j][k]$ 为处理完 $i$ 个字符 , 结尾字符为 $'a'+j$ , 结尾部分已重复出现了 $k$ 次的方案数。 刷表转移一下就好啦。 复杂度：$O(26 * 26 * nT)$ ## 1004 - King's Game 约瑟夫问题的一个变种，然而题目全部是在唬人，就是一个简单的递推。虽然我知道有人会打表。。。 我们看看裸的约瑟夫是怎么玩的：$n$ 个人，每隔 $k$ 个删除。 由于我们只关心最后一个被删除的人，并不关心最后的过程，所以，我们没有必要也不能够模拟整个过程。我们用递推解决。假设有$n$个人围成环，标号为$[0,n-1]$从$0$开始的好处是取模方便），每数$k$个人杀一个的情况下，最后一个存活的人的编号是$f[n]$。 我们有$f[1]=0$,这不需要解释。 接着考虑一般情况$f[n]$,第一个杀死的人的编号是$k-1$,杀死后只剩下$n-1$个人了，那么我们重新编号！ 原来编号为k的现在是$0$号，也就是编号之间相差$3$我们只要知道现在$n-1$个人的情况最后是谁幸存也就知道$n$个人的情况是谁幸存。幸运的是$f[n-1]$已经算出来了那$f[n]$就是在$f[n-1]$的基础上加上一个$k$即可不要忘记总是要取模。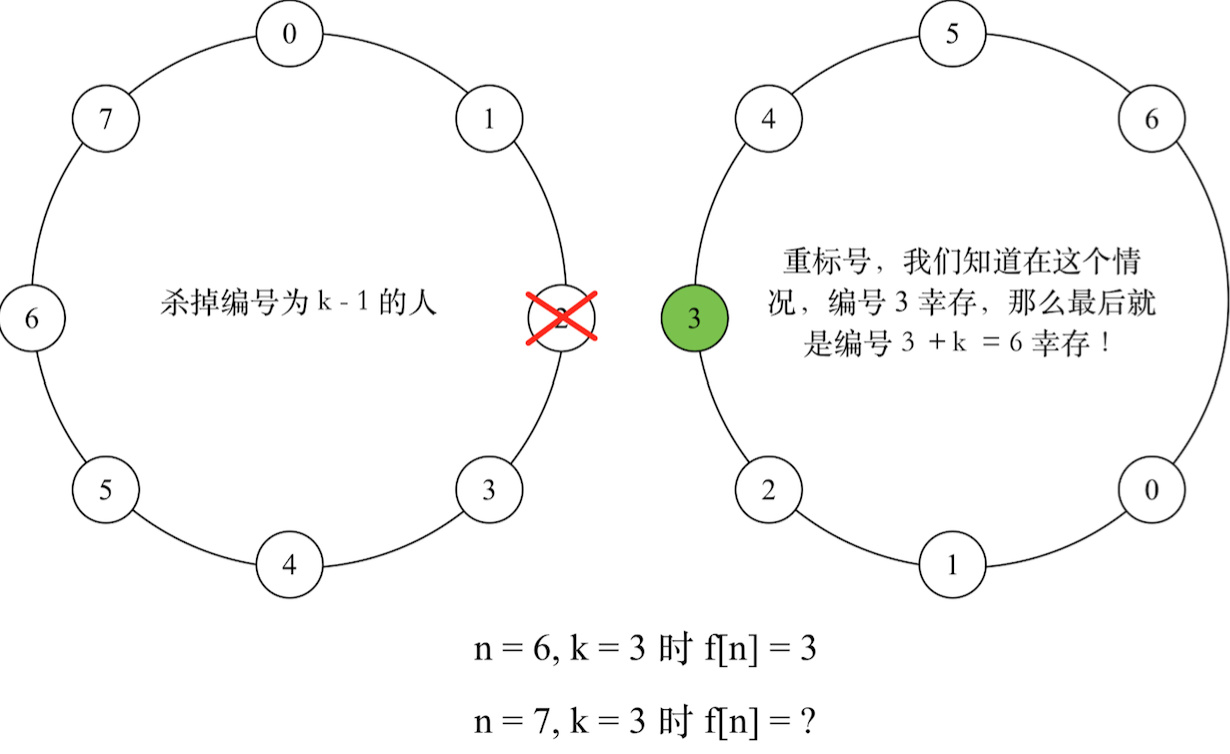  所以递推式子是： $f[i] = \begin{cases} & \text{ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } i=1 \\ & \text{ (f[i - 1] + k) mod i \ \ \ \ \ \ } other \end{cases}$ 此题只用在原版约瑟夫问题上加一维，由于依次隔 $1, 2, 3...n - 1$ 个人删除，所以用 $f[i][j]$ 表示 $i$ 个人，依次隔 $j, j + 1... j + i - 1$ 个人的幸存者标号。 根据刚才的重标号法，第一次 $j - 1$ 号出局，从 $j$ 开始新的一轮，从 $j + 1$ 开始清除，剩余 $i - 1$ 个人，也有递推式子： $f[i][j] = \begin{cases} & \text{ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } i=1 \\ & \text{ (f[i - 1][j+1] + j) mod i \ \ \ \ \ \ } other \end{cases}$ 答案就是 $f[n][1] + 1$（将标号转移到 $[1, n]$），问题轻松解决。 复杂度：预处理 $O(n^2)$，查询 $O(1)$，总复杂度 $O(n^2)$。由于可以滚动数组以及常数太小，所以 $n$ 给了 $5000$（其实是出题人不会别的算法嘿嘿嘿）。 ## 1005 - King's Pliot 这是一个费用流建模题 ， BC好久都没有费用流题了…… 这个题关键是要满足每天的飞行员数量充足 ， 那么可能是一开始就有的飞行员 ， 或者某飞行员休假归来 ， 或者新招募的飞行员。 将每一天拆成两个点 ，分别表示这一天开始时候飞行员的状态和这一天工作完成后飞行员的状态 ， 分别为 $X_i$ , $Y_i$ 先看看建图： 1. 从 S 向每个 $X_i$ 连一条容量为 $P_i$，费用为 $0$ 的有向边。 2. 从每个 $Y_i$向 T 连一条容量为 $P_i$，费用为 $0$ 的有向边。 3. 从 S 向 $Y_1$ 连一条容量为 $k$ ， 费用为 $0$ 的有向边。 4. 从 S 向每个 $Y_i(i\ge P)$ 连一条容量为无穷大，费用为 $Q$ 的有向边。(新招募的) 5. 从每个 $Xi$ 向 $Xi+1$ 连一条容量为无穷大，费用为 $0$ 的有向边。 6. 从每个$Yi$向$Yi+1$连一条容量为无穷大，费用为 $0$ 的有向边。 7. 对于每一个休假计划 ， 从每一个$X_i$ 向 $Y_{i+T_i}$ 连一条容量为无穷大费用为 $S_i$ 的有向边 然后开心的跑一跑最小费用最大流看一看是不是满流就可以判断是否可行啦…… 在此感谢Menci提供的帮助。

## LCP Array 如果$a_i=x$, 那么可以推断出$s_i=s_{i+1}=...=s_{i+x}$, 并且如果$a_i \ne 0$, 那么$a_{i+1}=a_i-1$, 利用第二个条件判断无解, 利用第一个条件划分等价类. 假设有$m$个等价类, 那么答案就是$26\cdot 25^{m-1}$ ## Shortest Path 你可以选择分类讨论, 但是估计可能会写漏一些地方. 只要抽出新增边的端点作为关键点, 建立一个新图, 然后跑一遍floyd就好了. 复杂度大概$O(6^2 \cdot m)$ ## Transform 注意到答案实际上只和$s \oplus t$有关, bfs预处理下从0到$x$的最短步数, 然后查询$O(1)$回答即可. ## Toposort 参考下普通的用堆维护求字典序最小拓扑序, 用某种数据结构维护入度小于等于$k$的所有点, 每次找出编号最小的, 并相应的减少$k$即可. 这个数据结构可以用线段树, 建立一个线段树每个节点$[l,r]$维护编号从$l$到$r$的所有节点的最小入度, 查询的时候只需要在线段树上二分, 找到最小的$x$满足入度小于等于$k$. 复杂度$O((n+m)\log n)$ ## Deletion ### 方法一: 考虑删掉的边的形态, 就是我们经常见到的环套树这种结构, 参考平时这种图给出的方法, 如果一个图的每个点的出边只有一条, 那么一定会构成环套树这种结构. 于是问题可以转化成, 给无向图的每条边定向, 使得出度最大点的出度最小 (每个点的出度大小对应了删的次数). 显然, 这个东西使可以二分的, 不妨设二分值为$x$. 考虑混合图的欧拉回路的做法, 利用网络流判合法. 先给每条无向边随便定向, 对于出度大于$x$的, 从源点连一条流量为$deg-x$的边, 对于出度小于$x$的, 从这个点连一条流量为$x-deg$的边到汇点. 对于原来图中的边, 流量为1加到网络流图中. 只要满流就是合法. ### 方法二: 类似方法一, 要求的无非是每条边的归属问题, 对于每条边$(a,b)$, 它可以属于$a$或者$b$, 那么新建一个节点表示这条边并和$a,b$都相邻, 这样就得到了一个二分图. 左边是原图中的节点, 右边是原图中的边. 二分每个左边每个节点的容量$k$, 如果右边的点能够完全匹配, 那么这个$k$就是可行的, 找到最小的$k$即可. 转化成二分图多重匹配问题. ### 方法三: 事实上这题存在$O(nm)$的做法, 只要在方法二的基础上继续改进就好了, 二分是没有必要的. 注意到每次增广的时候, 增光路中只有端点的容量会变化, 增广路中间的点的容量都不会变化. 那么之要每次增广到端点容量最小的那个点就好了.